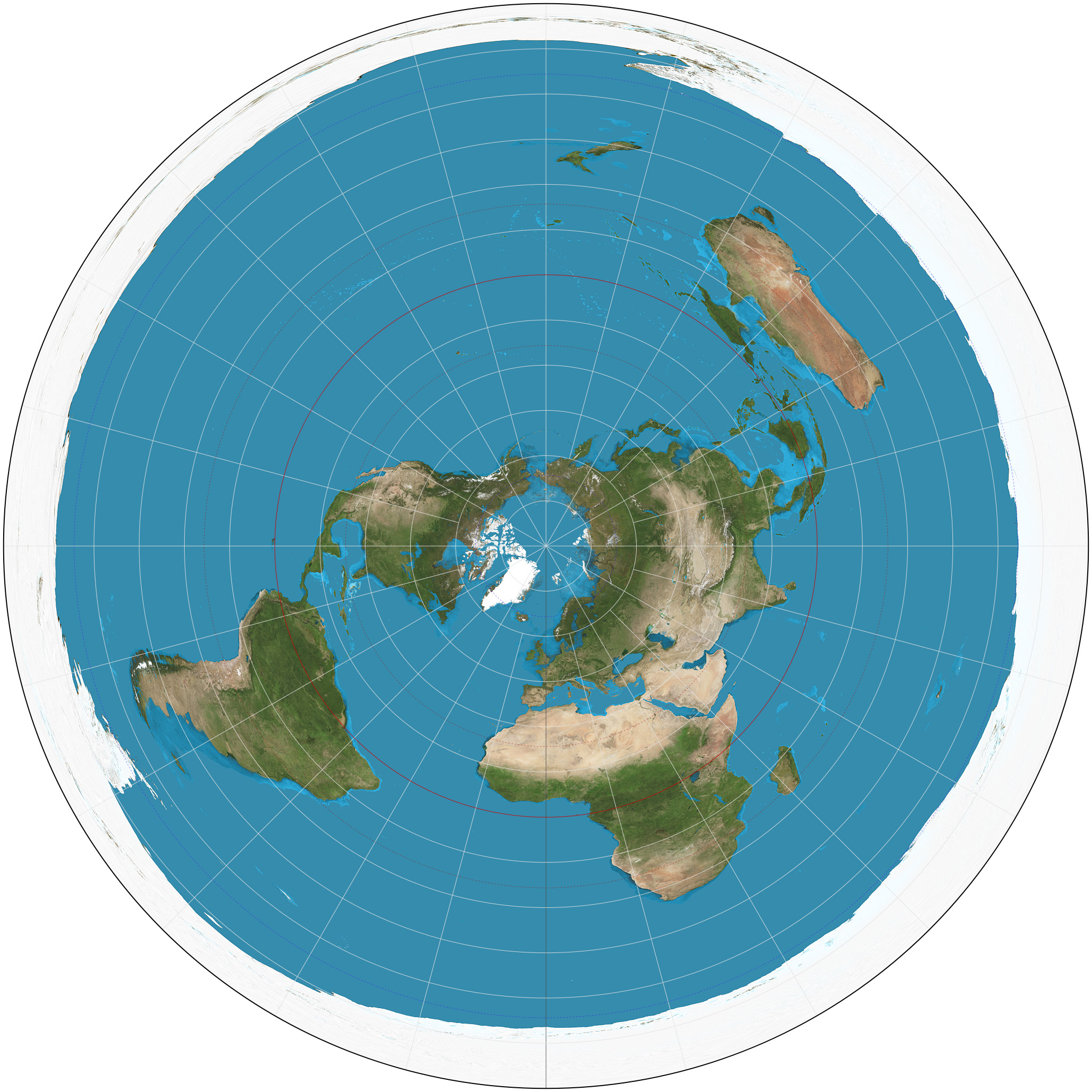
Recently the flat earth theory has had a resurgence among the conspiracy movement. There are thousands of videos on youtube which attempt to prove that the earth is flat. A key element to the flat earth theory is that the map on the United Nations flag is actually an accurate map of the world which is displayed openly for the purpose of mocking those who supposedly see through the purportedly massive conspiracy claiming that the earth is a globe. The map of the earth on the UN flag is called a polar azimuthal equidistant projection.
An Azimuthal equidistant projection skews the latitudinal distance while maintaining accurate longitudinal distance. That is, the distance along the longitudinal lines is accurate, or the distance from the center point to the edge is accurate. Only the distances from the center of the map are accurate. The further away from the center the more skewed the map is. That means at the furthest point away from the map, the area is stretched side-to-side or specifically circumferentially, so that the further away from the center point the larger the area looks. A quadrant near the edge of the map looks many times larger than a quadrant near the center of the map even though they are the same size.
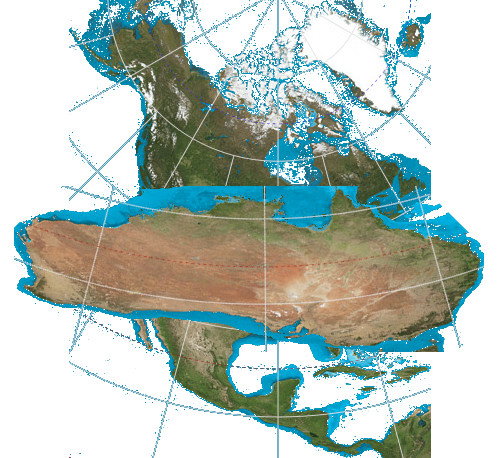
By comparing two similarly sized land masses which are different distances to the center we can easily see the foolishness of thinking that the Azimuthal equidistant projection is an accurate representation of the actual earth. For example, Australia is 2,969,907 square miles. The Contiguous United States is 3,119,884.69 square miles. North America is 9,540,000 square miles.
It is quite easy to see in an azimuthal equidistant projection that the true sizes of Australia and America are very inaccurate when compared with each other. In the azimuthal equidistant projection it appears that Australia is much larger than the contiguous United States even though it is approximately the same size in actuality.
Thus, the very map which the flat earth theorists purport to prove their theory actually disproves it.
Why is the flat earth theory being promoted to the extent that it is lately? It is because it is an easily disproved conspiracy theory which can be related to other conspiracy theories to discredit all of them as a whole.
George Bush Jr. once said, “THIS WOULD BE A LOT EASIER IF THIS WERE A DICTADORSHIP, AS LONG AS I’M THE DICTADOR”. It Would not surprise us in the least if, most politicians are thinking the same Way, including “OBAMA”.
“IS AMERICA TURNING INTO A FASCIST NATION”? Hitler said; He first needed the “ENABLING Act” EQUAL TO THE SO CALLED “PATRIOT Act”. A two-thirds majority was needed, since the law would actually alter the constitution. Hitler needed 31 non-Nazi votes to pass it. He got those votes from the Catholic Center Party after making a false promise to restore some basic rights already taken away by decree. That is HISTORY.
Are there some individuals in our GOVERNMENT trying to turn America into WWII “NAZI GERMANY?
The term “HOMELAND SECURITY” is just another way of saying “FATHERLAND SECURITY”. That is the same term that HITLER USED in NAZI GERMANY just before they started their GENOCIDAL SLAUGHTER AND MURDER OF MILLIONS in the name of SO CALLED “NATIONAL SECURITY”, another NAZI TERM they used as an excuse to kill those who could not defend themselves. That explains why they want to take our guns. It seems like the only way these EVIL people know how to deal with a population difficulty, is by “MURDERING” millions and millions of innocent people. IS MURDER THE ONLY SOLUTION THEY KNOW? They are POISONING the very AIR we breathe, the WATER we drink and the FOOD we eat. They are also fighting to take away our natural vitamins and minerals that our bodies need to fight CANCER and DISEASE. Out of curiosity, why are there so many “FASCIA”(NAZI) SYMBOLS in the house of CONGRESS, the SENATE and in all our STATE SHIELDS, SEALS and FLAGS? Also, why are we using an ADMIRALTY FLAG that belongs in our OCEANS and NOT on LAND, with the GOLD TRIM around it(THE CHOCK HOLD SYMBOL) OF MARTIAL LAW? Instead, why not use the PROPER civilian American FLAG without that EVIL GOLD TRIM? Thank you for your time. I am so glad that HITLER IS GONE. That is a GOOD THING. I hope? We really do not care if ALL the MEDIA CENSORS this information. We just want them to know, that WE ARE AWARE of the EVIL THEY ARE PLOTTING. By the way. Why did FATHERLAND SECURITY(HOMELAND SECURITY) PURCHASE SO MUCH AMO and 30,000 GUILLOTINES? GOD help us all. They are going to use NATO TROOPS to do the dirty deed so they can blame someone else. So sad. Pitiful…A new “HOLOCAUST” in AMERICA ???
Department of Homeland Security could just as easily be called (Bureau, Agency, Committee) of (Homeland, Fatherland, Motherland, State) Security. It translates to the Russian KGB.
THIS is the best they could come up with… to DETER people from believing in Flat Earth? Oh, when they’re scared they use any and all information from what bloggers and youtubers say- then come up with something in defense of their ‘programming’ of the population. No use trying…the ‘lost souls’ who are too heavily programmed that they’re comatose- will ALWAYS believe the program of the ‘system’…Those that have a chance to wake up- WILL. It’s the Aquarian age when all lies will be exposed and truth will come to light. The GREAT AWAKENING that you’re afraid of. You’re ONLY convincing the sleeping masses which will stay asleep anyway- a waste of time if you ask me. The awakening is happening- people are waking up EXPONENTIALLY and faster than ever before in the History of MANKIND…It’s snowballing. There’s o stopping it. Give up trying!
Funny because your Bible says the Earth doesn’t move and is in a fixed position surrounded by the Firmament. Nice try though…
Garbage. The map of the Flat Earth only exists one way, and placing the opposite view up from the globular southern polar region is a bias detractors way of imposing ridicule on the entire idea. The U.N. map is the accurate map, and the only map there is according to the Flat Earth theory. You didn’t disprove it, you just made fun of it. The oversimplification in the thoughts conveyed here are less for clarification and more for mockery’s sake. I’m not a Flat Earther, but I can’t stand the shallow attacker of the theory, nor the blatant obtuseness of the detraction machine unleashed on anyone daring to pose a sound alternate theory. You are not scientific, nor are you cleaver in any way. You’re just being a bit of a bastard.
You are missing the point. This map is their only model for their “flat earth”, and this post proves their model doesn’t work, as Australia is stretched way beyond its real life size.
If this “alternate theory” can’t propose a proper model that works and fits the size of the continents and oceans of earth, it is garbage.
So…I have a few questions of my own.
-Can you give me the IV, DV, CV’s and experiment that proves gravity or general relativity, please? Let me make this clear. Observed NATURAL phenomenon with a description of the CAUSE AND EFFECT.
-Then tell me the INHERENT shape of water.
-Show me water sticking to a spinning ball moving at 1037 mph at the equator in real time in a vacuum chamber.
-Define the conservation of angular momentum and define earth based coriolis effect….and then DEMONSTRATE the supposed 15 degree per hour drift assumed by earth based coriolis in real time in nature with things drifting away at the calculated and proper tangential speed. This is supposedly why the stars move in YOUR MODEL.
SO PROVE IT, THEN. DEMONSTRATE this drift in the inertial reference frame…the same REFERENCE FRAME your “second celestial pole” and your gas giant stars would be in “light years” away. In other words, PROVE AXIAL ROTATION OF THE EARTH.
-Describe the motion and location of this second celestial pole you speak of.
-Then tell me why a compass does not flip when you pass the equator to the south.
-Then Describe the difference between tangential speed and angular velocity.
-Show me water in a CONTAINER that does not lay flat or demonstrate something spinning attracting that water to the center of the object.
-Tell me how you measure the distance to a ball of gas or plasma…in a space vacuum and then describe how this does not violate the second law of thermodynamics.
-Show me air pressure without containment.
-Give me the equations for earth curvature and your terrestrial horizon LIMIT in distance.
-Repeat the black swan argument which you would need the terrestrial refraction limit equation to do.
-Describe the purpose of a MODUS TOLLENS argument.
-Prove the existence and show me absolute evidence of dark matter, space fabric/spacetime (not as a concept but as a palpable and observable phenomenon), a graviton and dark energy.
-Prove the sun is 93 million miles away and prove it is an actual object you CAN measure a distance to as this will be relevant in your gravitational equations for earth.
-Prove the gravitational constant (G) and show me where this is quantified in the Cavendish papers.
-Speaking of the Cavendish papers, show me where the density of the earth is quantified and then show me proof this is correct as you will need this value for the equation F=G(m1m2)/r^2 in order to get those two MASS values. The MASSES of 2 celestial objects.
-Show an example of air pressure without containment without using a begging the question fallacy of a mythical space vacuum. Then show how the V in your example would be measured in the equation PV=nRT.
-Prove the shape of the earth. Sphere? Oblate spheroid? Pear or other shape? It doesn’t seem academia has settled on a true shape.
-Then tell me how you would get the radius of anything not a sphere that would be required for both the equations in Einstein’s AND Newton’s gravity assertions.
-Prove the earth is actually a sphere and then with absolution and observable evidence (not math) a radius value of the earth if it is a sphere.
-Then prove the volume of the earth with this radius value that would be necessary to get the mass from the VOLUME of a sphere in the equation V=4/3(pi)r^3.
-Prove that Venus is the same size and density as earth as used as a comparison value to insert in the equation F=G(m1m2)/r^2 which is also used in Kepler’s orbital equations.
-Prove the masses in that equation which would require the radius, a true shape and a true volume.
-Prove the r value in that equation is a CONSTANT. (r being the distance between the two objects in an ~elliptical~ orbit…)
-Then tell me, does water evaporate towards the ground or up in defiance of the assertion that mass attracts mass?
-Tell me. Does the apple tree grow UP before the apple fell DOWN on Newton’s head?
-Prove nothing can move faster than light such as a thought or something as demonstrated by the observable instances of quantum entanglement. All 1875 documented instances of quantum entanglement that file 13’s General Relativity.
So…you think we live on a cartoon and that a cartoon legitimizes your globe earth nonsense?
You actually believe that a MODEL confirms anything? That cartoons somehow define reality?
And WHAT FLAT EARTH MODEL? WHICH ONE? The flat earth society of the disc in the space vacuum just like your flawed garbage spinning monkey ball cartoon?
You globers can’t even decide a shape, for God’s sake. NASA shows a perfect sphere from the second law of thermodynamics violating space vacuum where they cannot go.
WGS84 gives us the good old OBLATE SPHEROID.
Then you have Neil DeGrasse Tyson and his PEAR shaped earth.
Which is it, princess? Which MODEL do you believe?
And could you actually prove that one of your CARTOONS actually represent reality?
Haven’t a single glober than can do that. Ever.
Did any Flat Earther actually provide an answer to the Australia-America size discrepancy yet?
Nope.
Have any of you actually gotten out your measuring tape and walked out America and Australia? So, you’re just taking somebody’s word that it is the size they say it is?